Sudoku Puzzles - Solution methods
Solution methods
|
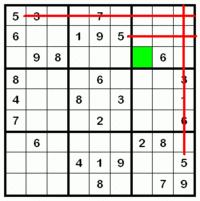
The 3x3 region in the top-right corner must contain a 5. By hatching across and up from 5s located elsewhere in the grid, the solver can eliminate all of the empty cells in the top-left corner which cannot contain a 5. This leaves only one possible cell (highlighted in green). |
The strategy for solving a puzzle may be regarded as comprising a combination of three processes: scanning, marking up, and analysing.
Scanning
Scanning is performed at the outset and periodically throughout the solution. Scans may have to be performed several times in between analysis periods. Scanning comprises two basic techniques, cross-hatching and counting, which may be used alternately:
- Cross-hatching: the scanning of rows (or columns) to identify which line in a particular region may contain a certain number by a process of elimination. This process is then repeated with the columns (or rows). For fastest results, the numbers are scanned in order of their frequency. It is important to perform this process systematically, checking all of the digits 1-9.
- Counting 1-9 in regions, rows, and columns to identify missing numbers. Counting based upon the last number discovered may speed up the search. It also can be the case (typically in tougher puzzles) that the value of an individual cell can be determined by counting in reverse - that is, scanning its region, row, and column for values it cannot be to see which is left.
Advanced solvers look for "contingencies" while scanning - that is, narrowing a number's location within a row, column, or region to two or three cells. When those cells all lie within the same row (or column) and region, they can be used for elimination purposes during cross-hatching and counting (Contingency example at Puzzle Japan). Particularly challenging puzzles may require multiple contingencies to be recognized, perhaps in multiple directions or even intersecting - relegating most solvers to marking up (as described below). Puzzles which can be solved by scanning alone without requiring the detection of contingencies are classified as "easy" puzzles; more difficult puzzles, by definition, cannot be solved by basic scanning alone.
Marking up
Scanning comes to a halt when no further numbers can be discovered. From this point, it is necessary to engage in some logical analysis. Many find it useful to guide this analysis by marking candidate numbers in the blank cells. There are two popular notations: subscripts and dots. In the subscript notation the candidate numbers are written in subscript in the cells. The drawback to this is that original puzzles printed in a newspaper usually are too small to accommodate more than a few digits of normal handwriting. If using the subscript notation, solvers often create a larger copy of the puzzle or employ a sharp or mechanical pencil. The second notation is a pattern of dots with a dot in the top left hand corner representing a 1 and a dot in the bottom right hand corner representing a 9. The dot notation has the advantage that it can be used on the original puzzle. Dexterity is required in placing the dots, since misplaced dots or inadvertent marks inevitably lead to confusion and may not be easy to erase without adding to the confusion.
Analysing
There are two main analysis approaches - elimination and what-if.
- In elimination, progress is made by successively eliminating candidate numbers from one or more cells to leave just one choice. After each answer has been achieved, another scan may be performed - usually checking to see the effect of the latest number. There are a number of elimination tactics. One of the most common is "unmatched candidate deletion". Cells with identical sets of candidate numbers are said to be matched if the quantity of candidate numbers in each is equal to the number of cells containing them. For example, cells are said to be matched within a particular row, column, or region if two cells contain the same pair of candidate numbers (p,q) and no others, or if three cells contain the same triple of candidate numbers (p,q,r) and no others. These are essentially coincident contingencies. These numbers (p,q,r) appearing as candidates elsewhere in the same row, column, or region in unmatched cells can be deleted.
- In the what-if approach, a cell with only two candidate numbers is selected and a guess is made. The steps above are repeated unless a duplication is found, in which case the alternative candidate is the solution. In logical terms this is known as reductio ad absurdum. Nishio is a limited form of this approach: for each candidate for a cell, the question is posed: will entering a particular number prevent completion of the other placements of that number? If the answer if yes, then that candidate can be eliminated. The what-if approach requires a pencil and eraser. This approach may be frowned on by logical purists as too much trial and error but it can arrive at solutions fairly rapidly.
Ideally one needs to find a combination of techniques which avoids some of the drawbacks of the above elements. The counting of regions, rows, and columns can feel boring. Writing candidate numbers into empty cells can be time-consuming. The what-if approach can be confusing unless you are well organised. The Holy Grail is to find a technique which minimises counting, marking up, and rubbing out.
Wikipedia, the free encyclopedia.
- autentifică-te pentru a adăuga comentarii