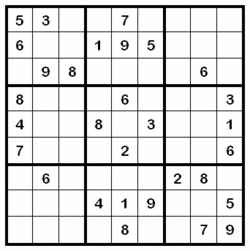
SuDoku
Mathematics of Sudoku
Mathematics of Sudoku
The general problem of solving Sudoku puzzles on n2 x n2 boards of n x n blocks is known to be NP-complete. This gives some vague indication of why Sudoku is hard to solve, but on boards of finite size the problem is finite and can be solved by a deterministic finite automaton that knows the entire game tree.
Sudoku History
History
The puzzle was first published in New York in the late 1970s by the specialist puzzle publisher Dell Magazines in its magazine Math Puzzles and Logic Problems, under the title Number Place. The person who designed the puzzle and composed the first of its kind is not recorded, but it was probably Walter Mackey, one of Dell's puzzle constructors. The puzzle was introduced in Japan by Nikoli in the paper Monthly Nikolist in April 1984 as Suuji wa dokushin ni kagiru (数字は独身に限る), which can be translated as "the numbers must be single" or "the numbers must occur only once" (独身 literally means "single; celibate; unmarried"). The puzzle was named by Kaji Maki (鍜治 真起), the president of Nikoli. At a later date, the name was abbreviated to Sudoku (数独, pronounced SUE-dough-coo; sū = number, doku = single); it is a common practice in Japanese to take only the first kanji of compound words to form a shorter version. In 1986, Nikoli introduced two innovations which guaranteed the popularity of the puzzle: the number of givens was restricted to no more than 30 and puzzles became "symmetrical" (meaning the givens were distributed in rotationally symmetric cells). It is now published in mainstream Japanese periodicals, such as the Asahi Shimbun. Nikoli still holds the trademark for the name Sudoku; other publications (at least in Japan) use other names.
Sudoku Explained
Sudoku (Japanese: 数独,, sūdoku), sometimes spelled Su Doku, is a placement puzzle, also known as Number Place in the United States. The aim of the puzzle is to enter a number from 1 through 9 in each cell of a grid, most frequently a 9×9 grid made up of 3×3 subgrids (called "regions"), starting with various numbers given in some cells (the "givens"). Each row, column and region must contain only one instance of each number. Completing the puzzle requires patience and modest logical ability (although some puzzles can be very difficult). Its classic grid layout is reminiscent of other newspaper puzzles like crosswords and chess problems. First published in the United States, Sudoku initially became popular in Japan in 1986 and attained international popularity in 2005.
Sudoku Construction
Construction
It is commonly believed that Dell Number Place puzzles are computer-generated; they typically have over 30 givens placed in an apparently random scatter, some of which can possibly be deduced from other givens. They also have no authoring credits. Wei-Hwa Huang claims that he was commissioned by Dell to write a Number Place puzzle generator in the winter of 2000; prior to that, he was told, the puzzles were hand-made. The puzzle generator was written in Visual C++, and although had options to generate a more Japanese-style puzzle, with symmetry constraints and fewer numbers, Dell opted not to use those features. Presumably the puzzles since then still use that program, although it is hard to tell.
Sudoku Puzzles - Computer solutions
Computer solutions
For computer programmers it is relatively simple to build a backtracking search. Typically this would assign a value (say, 1, or the nearest available number to 1) to the first available cell (say, the top left hand corner) and then move on to assign the next available value (say, 2) to the next available cell. This continues until a duplication is discovered in which case the next alternative value is placed in the last field changed. Although far from computationally efficient, this method will find the solution, given sufficient computation time. A more efficient program could keep track of potential values for cells, eliminating impossible values until only one value remains for a cell, then filling that cell in and using that information for more eliminations, and so on until the puzzle is solved. This more closely emulates the way a human would solve the puzzle without resorting to guesses.